
5.1 - Introduction to Hypothesis Testing.4.6 - Impact of Sample Size on Confidence Intervals.4.4.2.2 - Example: Difference in Dieting by Biological Sex.4.4.2.1 - Example: Correlation Between Quiz & Exam Scores.4.4.1.2 - Example: Difference in Mean Commute Times.4.4.1.1 - Example: Proportion of Lactose Intolerant German Adults.4.3.2 - Example: Bootstrap Distribution for Difference in Mean Exercise.4.3.1 - Example: Bootstrap Distribution for Proportion of Peanuts.4.2.1 - Interpreting Confidence Intervals.4.2 - Introduction to Confidence Intervals.4.1.1.2 - Coin Flipping (One Proportion).3.5 - Relations between Multiple Variables.3.4.2.2 - Example of Computing r by Hand (Optional).3.4.2.1 - Formulas for Computing Pearson's r.3.3 - One Quantitative and One Categorical Variable.2.2.6 - Minitab: Central Tendency & Variability.2.2.1 - Graphs: Dotplots and Histograms.2.1.3.2.5.1 - Advanced Conditional Probability Applications.2.1.3.2.1 - Disjoint & Independent Events.2.1.2.1 - Minitab: Two-Way Contingency Table.1.2.2.1 - Minitab: Simple Random Sampling.1.1.2 - Explanatory & Response Variables.1.1.1 - Categorical & Quantitative Variables.The \(y\) intercept is the location on the \(y\) axis where the line passes through this is the value of \(y\) when \(x\) equals 0. For every one unit increase in \(x\) the predicted value of \(y\) increases by the value of the slope. A negative slope indicates a line moving from the top left to bottom right. A positive slope indicates a line moving from the bottom left to top right. The slope is a measure of how steep the line is in algebra this is sometimes described as "change in \(y\) over change in \(x\)," or "rise over run". You may recall from an algebra class that the formula for a straight line is \(y=mx+b\), where \(m\) is the slope and \(b\) is the \(y\)-intercept. The "linear" part is that we will be using a straight line to predict the response variable using the explanatory variable. If there are two or more explanatory variables, then multiple linear regression is necessary. The "simple" part is that we will be using only one explanatory variable.
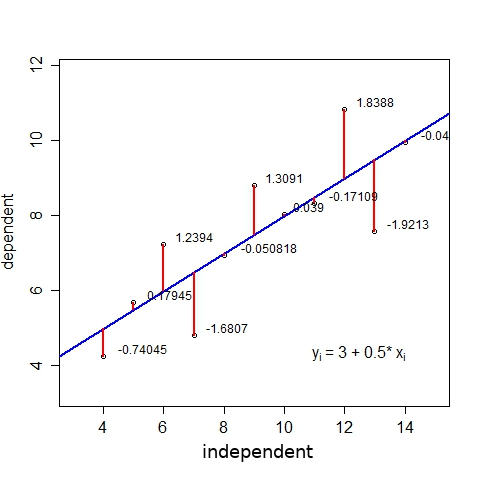
In this lesson we will be learning specifically about simple linear regression. Recall from Lesson 3, regression uses one or more explanatory variables (\(x\)) to predict one response variable (\(y\)).


 0 kommentar(er)
0 kommentar(er)
